Question

Which points lie on the line that passes through point P and

is parallel to the given line? Select three options.
(-4,2)
(-1,3)
(-2, 2)
(4,2)
(-5, -1)

Answer 1

(-5,-1)

Explanation:

First, draw a parallel line to the blue one that has a slope of over 1 to the right and up 1.

Second, look at the new line and see if any of the points are on the line.

All of the other point do not fall on the new line.

Answer 2

Option 2nd , 3rd and 5th are correct.

Explanation:

Given:

Given line passes through points ( -2 , -4 ) and ( 4 , 2 )

Coordinate of the Point P( 0 , 4 )

To find: Point which lie on the line parallel to given line and passes through point P.

Slope of the given line =
`(y_2-y_1)/(x_2-x_1)\:=\:(-4-2)/(-2-4)\:=\:(-6)/(-6)\:=\:1`

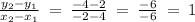
We know that slope of parallel lines ara equal.

So, Using Slope-Point form we get equation of line,

`y-y_1=m(x-x_1)`

y - 4 = 1 ( x - 0 )

y - 4 = x

x - y = -4

Option 1:

x = -4 , y = 2

LHS = -4 - 2 = -6 ≠ RHS

Thus, This is not required point.

Option 2:

x = -1 , y = 3

LHS = -1 - 3 = -4 = RHS

Thus, This is required point.

Option 3:

x = -2 , y = 2

LHS = -2 - 2 = -4 = RHS

Thus, This is required point.

Option 4:

x = 4 , y = 2

LHS = 4 - 2 = 2 ≠ RHS

Thus, This is not required point.

Option 5:

x = -5 , y = -1

LHS = -5 - (-1) = -4 = RHS

Thus, This is required point.

Therefore, Option 2nd , 3rd and 5th are correct.