Question

Island A is 250 miles from island B. A ship captain travels 260 miles from island A and then finds that he is off course and 160 miles from island B. What bearing should he turn to, so he is heading straight towards island B?

A. 111.65
B. 119.84
C. 21.65
D. 135.53

Answer 1

Answer: Option 'a' is correct.

Explanation:

Since we have given that

AB = 250 feet

AC = 260 feet

BC = 160 feet

We need to find the angle C that is heading straight towards island B.

We will apply "Law of cosine":

`\cos C=(a^2+b^2-c^2)/(2ab)\\\\\cos C=(160^2+260^2-250^2)/(2* 160* 260)\\\\\cos C=0.368\\\\C=\cos^(-1)(0.368)\\\\C=68.40^\circ`

Exterior angle would be

`180-68.40=111.65^\circ`

Hence, Option 'a' is correct.

Answer 2

A. 111.65

Explanation:

This scenario can be interpreted like a triangle ABC where A and B are islands and C is the point from where the captain is 160 miles from island B.

a = 160

b = 260

c = 250

Law of cosines

`c^2 = a^2 + b^2 - 2(ab)Cos(C)\\Arranging\ as\\2ab \ cos\ C = a^2+b^2-c^2\\2(160)(260)\ cos\ C = (160)^2+(260)^2- (250)^2\\83200\ cos\ C=25600+67600-62500\\83200\ cos\ C=30700\\cos\ C= (30700)/(83200)\\cos\ C=0.36899\\C = arccos\ (0.36899)\\C = 68.35`

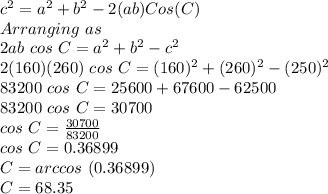
The internal angle is 68.35°

We have to find the external angle to find the bearing the captain should turn

Using the rule of supplimentary angles:

The external angle = 180 - 68.35 = 111.65°

Therefore, the captain should turn 111.65° so that he would be heading straight towards island B.

Hence, option 1 is correct ..