Question

Find the length of "a", to
the nearest tenth, using
the Pythagorean Theorem.
Enter

Answer 1

`√(28) \approx 5.3`

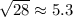
Explanation:

The Pythagorean Theorem says if you have a right triangle, then relationship between the three sides is the sum of the square of each leg is the hypotenuse squared.

So
`a^2+b^2=c^2`

where a and b are legs and c is the hypotenuse.

Plug in your a,b, and c. In this case it is a,6, and 8.

This means we have

`a^2+6^2=8^2`

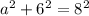
Simplify where you can before we begin the solving (the moving around of things to other sides).

`a^2+36=64`

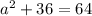
Now time for the solving. We are first going to get
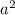`a^2` by itself.

To do this, we just need to subtract 36 on both sides giving us:

`a^2=64-36`

`a^2=28`

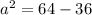
Now to get rid of the square on a, just square root both sides:

`a=√(28)`.