What graph represents the compound inequality x<5/4 or x>5/2

Question

asked Mar 10, 2020 151k views

2 Answers

SimonRH · Answer 1 · 2020-03-12T15:34:17+0000

Answer:

SECOND graph.

Explanation:

Given compound inequality,

$x \leq (5)/(4)\text{ or }x \geq (5)/(2)$

$\because (5)/(4)=1.25\text{ or }(5)/(2)=2.5$

$\implies x \leq 1.25\text{ or }x\geq 2.5$

If x ≥ 1.25

In the number line closed circle on 1.25 and shaded left side from 1.25,

If x ≤ 2.5

In the number line closed circle on 2.5 and shaded right side from 2.5

Hence, SECOND option is correct.

Gosulove · Answer 2 · 2020-03-16T09:27:56+0000

For this case we have to:

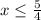$x \leq \frac {5} {4}$ : Represents all values less than or equal to
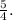
$\frac {5} {4}.$

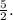
$x \geq \frac {5} {2}$ : Represents all values greater than or equal to
$\frac {5} {2}.$

As the inequalities include the sign "=", then the borders of the graphs will be closed.

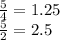
$\frac {5} {4} = 1.25\\\frac {5} {2} = 2.5$

The word "or" indicates one solution or the other, so the correct option is graph B

ANswer:

Option B