Answer : The value of
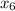 is
is
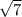 .
.
Explanation :
As we are given 6 right angled triangle in the given figure.
First we have to calculate the value of
 .
.
Using Pythagoras theorem in triangle 1 :
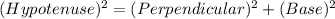
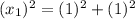


Now we have to calculate the value of
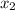 .
.
Using Pythagoras theorem in triangle 2 :
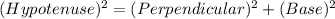

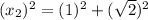
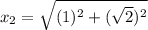

Now we have to calculate the value of
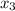 .
.
Using Pythagoras theorem in triangle 3 :
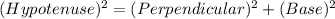
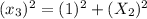
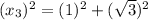
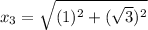

Now we have to calculate the value of
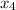 .
.
Using Pythagoras theorem in triangle 4 :
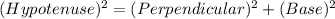
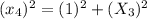
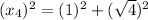
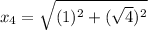

Now we have to calculate the value of
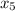 .
.
Using Pythagoras theorem in triangle 5 :
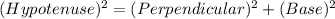

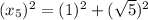
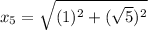
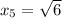
Now we have to calculate the value of
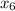 .
.
Using Pythagoras theorem in triangle 6 :
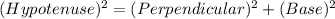
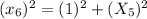

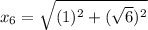

Therefore, the value of
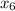 is
is
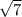 .
.