Answer:
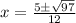
Explanation:
First step is to arrange so it is in the form
 .
.
We have
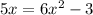 .
.
Add we really need to do is subtract 5x on both sides:
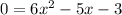 .
.
Now let's compare
 to
to
 .
.
We have
 .
.
The quadratic formula is
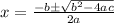 .
.
I like to break this into parts:
Part 1: Find
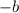 .
.
Part 2: Find
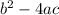 .
.
Part 3: Find
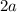 .
.
Answering the parts:
Part 1:
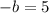 since
since
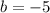 .
.
Part 2:
 .
.
Part 3:
 .
.
Now our formula in terms of my parts looks like this:
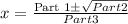
Our formula with my parts evaluated looks like this:
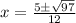 .
.