Question

Which equation represents a circle that contains the point (-2, 8) and has a center at (4, 0)

Answer 1

A

Explanation:

Answer 2

Option 1:(x-4)^2+y^2=100

Explanation:

Given center = (h,k) = (4,0)

The point (-2,8) lies on circle which means the distance between the point and center will be equal to the radius.

So,

The distance formula will be used:

`d = \sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)} \\=\sqrt{(4+2)^(2)+(0-8)^(2)}\\=\sqrt{(6)^(2)+(-8)^(2)}\\=√(36+64)\\ =√(100)\\ =10\ units`

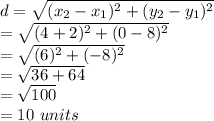
Hence radius is 10.

The standard form of equation of circle is:

(x-h)^2+(y-k)^2 = r^2

Putting the values

(x-4)^2+(y-0)^2=10^2

(x-4)^2+y^2=100

Hence option 1 is correct ..