Question

Which method would you use to prove that the two triangles are congruent?

SAS
SSS
AAS
ASA

Answer 1

Answer: The correct option is (A) SAS.

Step-by-step explanation: We are given to select the method that would be used to prove that the two triangles are congruent.

Let us name the given triangles as ABC and EBD as shown in the attached figure below.

Then, according to the given information, we have

`AB=BD\\\intertext{and}\\BC=EB.`

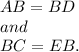
Also, ∠ABC and ∠EBD are vertically opposite angles, so they must have equal measures.

That is,

`m\angle ABC=m\angle EBD.`

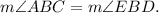
So, in triangles ABC and EBD, we have

`AB=BD,\\\\BC=EB\\\\\intertext{and}\\m\angle ABC=m\angle BED.`

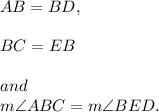
That is, two sides and the included angle of one triangle are congruent to the corresponding two sides and the included angle of the other triangle.

Therefore, by side-angle-angle postulate, the two triangles are congruent.

Thus,

ΔABC ≅ ΔEBD (SAS postulate).

Option (A) is CORRECT.