Question

Solve x^2-8x=3 by completing the square. Which is the solution set of the equation

Answer 1

{-0.36, 8.36) to the nearest hundredth.

Explanation:

x^2 - 8x = 3

(x - 4)^2 - 16 = 3

(x - 4)^2 = 19

Taking square roots:

x - 4 = +/- √19

x = 4 +/- √19

x = {-0.36, 8.36} to nearest 1/100.

Answer 2

For this case we have the following expression:

`x ^ 2-8x = 3`

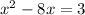
We must complete squares.

So:

We divide the middle term between two and we square it:

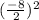`(\frac {-8} {2}) ^ 2`, then:

`x ^ 2-8x + (\frac {-8} {2}) ^ 2 = 3 + (\frac {-8} {2}) ^ 2\\x ^ 2-8x + (- 4) ^ 2 = 3 + 16`

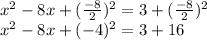
We have to, by definition:

`(a-b) ^ 2 = a ^ 2-2ab + b ^ 2`

Then, rewriting:

(
`(x-4) ^ 2 = 19`

To find the roots, we apply square root on both sides:

`x-4 = \sqrt {19}`

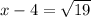
We have two solutions:

`x_ {1} = \sqrt {19} +4\\x_ {2} = - \sqrt {19} +4`

Answer:

(
`(x-4) ^ 2 = 19\\x_ {1} = \sqrt {19} +4\\x_ {2} = - \sqrt {19} +4`