Answer: The length of the indicated segment is 14.45 units.
Step-by-step explanation: We are given to find the length of the indicated segment.
From the figure, we note that
A chord is bisected by the radius of the circle that makes a right-angled triangle with hypotenuse measuring 16.1 units and the other two sides measures x units and 7.1 units.
Using Pythagoras theorem, we get
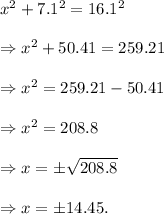
Since x is the length of side of a triangle, so we get
x = 14.45.
Thus, the length of the indicated segment is 14.45 units.