Question

Indicate the equation of the given line in standard form. Show all your work for full credit. the line containing the median of the trapezoid whose vertices are R(-1,5)S(1,8) T(7,-2) U(2,0)

Answer 1

* The equation of the median of the trapezoid is 10x + 6y = 39

Explanation:

* Lets explain how to solve the problem

- The slope of the line whose end points are (x1 , y1) , (x2 , y2) is

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

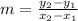
- The mid point of the line whose end point are (x1 , y1) , (x2 , y2) is

`((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2))`

- The standard form of the linear equation is Ax + BC = C, where

A , B , C are integers and A , B ≠ 0

- The median of a trapezoid is a segment that joins the midpoints of

the nonparallel sides

- It has two properties:

# It is parallel to both bases

# Its length equals half the sum of the base lengths

* Lets solve the problem

- The trapezoid has vertices R (-1 , 5) , S (! , 8) , T (7 , -2) , U (2 , 0)

- Lets find the slope of the 4 sides two find which of them are the

parallel bases and which of them are the non-parallel bases

# The side RS

∵
`m_(RS)=(8-5)/(1 - (-1))=(3)/(2)`

# The side ST

∵
`m_(ST)=(-2-8)/(7-1)=(-10)/(6)=(-5)/(3)`

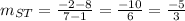
# The side TU

∵
`m_(TU)=(0-(-2))/(2-7)=(2)/(-5)=(-2)/(5)`

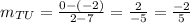
# The side UR

∵
`m_(UR)=(5-0)/(-1-2)=(5)/(-3)=(-5)/(3)`

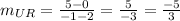
∵ The slope of ST = the slop UR

∴ ST// UR

∴ The parallel bases are ST and UR

∴ The nonparallel sides are RS and TU

- Lets find the midpoint of RS and TU to find the equation of the

median of the trapezoid

∵ The median of a trapezoid is a segment that joins the midpoints of

the nonparallel sides

∵ The midpoint of RS =
`((-1+1)/(2),(5+8)/(2))=(0,(13)/(2))`

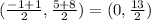
∵ The median is parallel to both bases

∴ The slope of the median equal the slopes of the parallel bases = -5/3

∵ The form of the equation of a line is y = mx + c

∴ The equation of the median is y = -5/3 x + c

- To find c substitute x , y in the equation by the coordinates of the

midpoint of RS

∵ The mid point of Rs is (0 , 13/2)

∴ 13/2 = -5/3 (0) + c

∴ 13/2 = c

∴ The equation of the median is y = -5/3 x + 13/2

- Multiply the two sides by 6 to cancel the denominator

∴ The equation of the median is 6y = -10x + 39

- Add 10x to both sides

∴ The equation of the median is 10x + 6y = 39

* The equation of the median of the trapezoid is 10x + 6y = 39