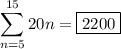If
 is a number that is both divisible by 4 and 5, then
is a number that is both divisible by 4 and 5, then
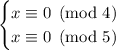
4 and 5 are coprime, so we can use the Chinese remainder theorem to solve this system and find that
 is a solution to the system, where
is a solution to the system, where
 is any integer. Simply put, any multiple of 20 fits the bill.
is any integer. Simply put, any multiple of 20 fits the bill.
Now, there are 11 numbers between 100 and 300 that are divisible by 20 (100, 120, 140, and so on). We have
 when
when
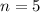 , so the sum we want to compute is
, so the sum we want to compute is