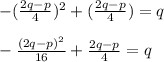Question

Find the relation independent of y for the following equation
-2y^2-2y=p
-y^2+y=q

Answer 1

`-((2q-p)^(2))/(16) +(2q-p)/(4)=q`

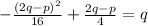
Explanation:

The given equations are:

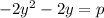`-2y^(2)-2y=p` Equation 1

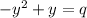`-y^(2)+y=q` Equation 2

Multiplying the Equation 2 with -2, we get:

`-2(-y^(2)+y)=-2(q)\\`

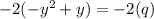
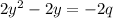`2y^(2)-2y=-2q` Equation 3

Adding Equation 1 and Equation 3, we get:

`-2y^(2)-2y + (2y^(2)-2y)=p+(-2q)\\\\ -2y^(2)-2y + 2y^(2)-2y=p-2q\\\\ -4y=p-2q\\\\ y= (p-2q)/(-4)\\\\ y=(2q-p)/(4)`

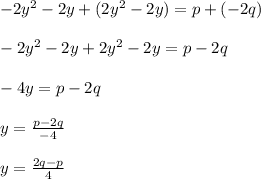
Using this value of y, in either of the equations will give the relation independent of y.

Using the value of y in Equation 2, we get:

`-((2q-p)/(4))^(2)+((2q-p)/(4) )=q\\\\ -((2q-p)^(2))/(16) +(2q-p)/(4)=q`