Question

The initial activity of 37Ar is 8540 disintegrations per minute. After 10.0 days, the activity is 6990 disintegrations per minute. what is the activity after 47.2 days?​

Answer 1

Approximately 3318 disintegrations per minute.

Step-by-step explanation:

The activity
`A` of a radioactive decay at time
`t` can be found with the following equation:

`\displaystyle A(t) = A_0 \cdot \mathrm{e}^(-\lambda\cdot t)`.

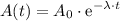In this equation,

• 
  `\mathrm{e}` is the natural base.
  `\mathrm{e}\approx 2.71828`.
• 
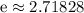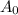  `A_0` is the initial activity of the decay. For this question,
  `A_0 = \rm 8540\; min^(-1)`.
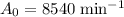• The decay constant
  `\lambda` of this sample needs to be found.

The decay constant here can be found using the activity after 10 days. As long as both times are in the same unit (days in this case,) conversion will not be necessary.

`A(10) = A_0\cdot \mathrm{e}^(\rm -\lambda * 10\;day)= (\mathrm{8540\; min^(-1)})\cdot \mathrm{e}^(\rm -\lambda * 10\;day)`.

`A(10) = \rm 6690\; min^(-1)`.

`\displaystyle \frac{\rm 6690\; min^(-1)}{\mathrm{8540\; min^(-1)}} = \mathrm{e}^(\rm -\lambda * 10\;day)`

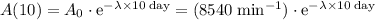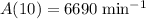Apply the natural logarithm to both sides of this equation.

`\displaystyle \ln{\left(\frac{\rm 6690\; min^(-1)}{\mathrm{8540\; min^(-1)}}\right)} = \ln{\left(\mathrm{e}^(\rm -\lambda * 10\;day)\right)}`.

`\displaystyle \rm -\lambda \cdot (10\;day) = \ln{\left(\frac{\rm 6690\; min^(-1)}{\mathrm{8540\; min^(-1)}}\right)}`.

`\displaystyle \rm \lambda= \rm \frac{\displaystyle \ln{\left(\frac{\rm 6690\; min^(-1)}{\mathrm{8540\; min^(-1)}}\right)}}{-10 \; day} \approx 0.0200280\; day^(-1)`.

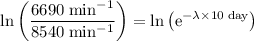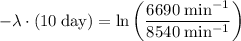Note that the unit of the decay constant
`\lambda` is
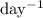`\rm day^(-1)` (the reciprocal of days.) The exponent
`-\lambda \cdot t` should be dimensionless. In other words, the unit of
`t` should also be days. This observation confirms that there's no need for unit conversion as long as the two times are in the same unit.

Apply the equation for decay activity at time
`t` to find the decay activity after 47.2 days.

`\displaystyle \begin{aligned}A(t)& = A_0 \cdot \mathrm{e}^(-\lambda\cdot t)\\&\approx \rm \left(8540\; min^(-1)\right)\cdot \mathrm{e}^{-0.0200280\; day^(-1)* 47.2\;day}\\&\approx \rm 3318\; min^(-1)\end{aligned}`.

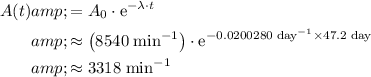By dimensional analysis, the unit of activity here should also be disintegrations per minute. The activity after 47.2 days will be approximately 3318 disintegrations per minute.