Question

Given h(x) = |x+3| -5

•Identify the parent function f

•Describe the sequence of transformation from f to h

Answer 1

The parent function f(x) is equal to
`f\left(x\right)=\left|x\right|`

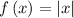
The translations is 3 units to the left and 5 units down

Explanation:

we have

`h\left(x\right)=\left|x+3\right|-5`

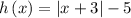
The vertex of the function h(x) is the point (-3,-5)

we know that the parent function f(x) is equal to

`f\left(x\right)=\left|x\right|`

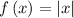
The vertex of the function f(x) is the point (0,0)

so

The rule of the transformation of f(x) to h(x) is equal to

(x,y) -----> (x-3,y-5)

That means ----> The translations is 3 units to the left and 5 units down