Answer:
The line containing the midpoints of two sides of a triangle is parallel to the third side ⇒ proved down
Explanation:
* Lets revise the rules of the midpoint and the slope to prove the
problem
- The slope of a line whose endpoints are (x1 , y1) and (x2 , y2) is
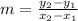
- The mid-point of a line whose endpoints are (x1 , y1) and (x2 , y2) is

* Lets solve the problem
- PQR is a triangle of vertices P (0 , 0) , Q (2a , 0) , R (2b , 2c)
- Lets find the mid-poits of PQ called A
∵ Point P is (x1 , y1) and point Q is (x2 , y2)
∴ x1 = 0 , x2 = 2a and y1 = 0 , y2 = 0
∵ A is the mid-point of PQ
∴
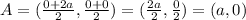
- Lets find the mid-poits of PR which called B
∵ Point P is (x1 , y1) and point R is (x2 , y2)
∴ x1 = 0 , x2 = 2b and y1 = 0 , y2 = 2c
∵ B is the mid-point of PR
∴
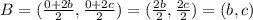
- The parallel line have equal slopes, so lets find the slopes of AB and
QR to prove that they have same slopes then they are parallel
# Slope of AB
∵ Point A is (x1 , y1) and point B is (x2 , y2)
∵ Point A = (a , 0) and point B = (b , c)
∴ x1 = a , x2 = b and y1 = 0 and y2 = c
∴ The slope of AB is
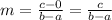
# Slope of QR
∵ Point Q is (x1 , y1) and point R is (x2 , y2)
∵ Point Q = (2a , 0) and point R = (2b , 2c)
∴ x1 = 2a , x2 = 2b and y1 = 0 and y2 = 2c
∴ The slope of AB is
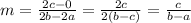
∵ The slopes of AB and QR are equal
∴ AB // QR
∵ AB is the line containing the midpoints of PQ and PR of Δ PQR
∵ QR is the third side of the triangle
∴ The line containing the midpoints of two sides of a triangle is parallel
to the third side