Question

Find the quadratic function that fits curve below. Select the correct answer.

Answer 1

Hello!

The answer is:

The quadratic function that fits the given picture is:

`y=-3x^(2)+13x-5`

Why?

We can solve the problem and find the correct function that fits the curve below by finding which function intercepts the y-axis at -5 (we can see it from the picture), also, we need to look for a function that represents a parabola opening upwards. We need to remember that when a parabola is opening upwards, its quadratic term coefficient is negative.

So, we can see that from the given functions, the only function that represents a parabola opening upwards and its y-intercept is located at y equal to -5 is the second option:

`y=-3x^(2)+13x-5`

We have that :

`a=-3(negative)\\b=13\\c=-5(y-intercept)`

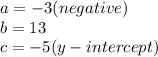
We can see that the quadratic term (a) is negative, and the quadratic function intercepts the y-axis at y equal to -5.

Hence, the answer is:

The quadratic function that fits the given picture is:

`y=-3x^(2)+13x-5`

Have a nice day!

Note: I have attached a picture for better understanding.