2 Answers

Blareprefix · Answer 1 · 2020-07-28T06:32:46+0000

Hello!

The answer is:

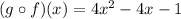
$(g \circ f)(x)=4x^(2)-4x-1$

To solve the problem, we need to remember that composing functions means evaluate a function into another different function.

Also, we need to remember how to solve the following notable product:

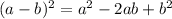
(a-b)^(2)=a^(2)-2ab+b^(2)

We have that:

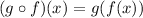
$(g \circ f)(x)=g(f(x))$

Now, we are given the equations:

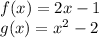
$f(x)=2x-1\\g(x)=x^(2)-2$

So, composing we have:

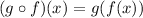
$(g \circ f)(x)=g(f(x))$

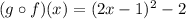
$(g \circ f)(x)=(2x-1)^(2)-2$

Now, we have to solve the notable product:

$(g \circ f)(x)=((2x)^(2)-2(2x*1)+1^(2))-2$

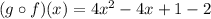
$(g \circ f)(x)=4x^(2)-4x+1-2$

Hence, we have that:

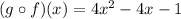
$(g \circ f)(x)=4x^(2)-4x-1$

Have a nice day!