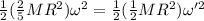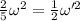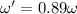Question

A uniform solid sphere of mass M and radius R rotates with an angular speed ω about an axis through its center. A uniform solid cylinder of mass M, radius R, and length 2R rotates through an axis running through the central axis of the cylinder. What must be the angular speed of the cylinder so it will have the same rotational kinetic energy as the sphere?

Answer 1

w_cyl = ±√(4/5) ω

Step-by-step explanation:

Kinetic energy

E = (1/2)Iw²

where I is the moment of inertia and w the angular frequency of rotation.

The moment of inertia of a solid sphere of mass M and radius R is:

I = (2/5)MR²,

Solid cylinder is of mass M and radius R

I = (1/2)MR²

Equate the energies through

(1/2)×(2/5) M R²× (w_sphere)² = (1/2)× (1/2) MR² × (w_cyl)²

(w_cyl)² = (4/5)(w_sphere)²

w_cyl = ±√(4/5) ω

The energy of rotation is independent of the direction of rotation

Answer 2

`\omega' = 0.89\omega`

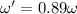
Step-by-step explanation:

Rotational inertia of uniform solid sphere is given as

`I = (2)/(5)MR^2`

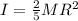
now we have its angular speed given as

angular speed =
`\omega`

now we have its final rotational kinetic energy as

`KE = (1)/(2)((2)/(5)MR^2)\omega^2`

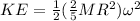
now the rotational inertia of solid cylinder about its axis is given by

`I = (1)/(2)MR^2`

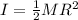
now let say its angular speed is given as

angular speed =
`\omega'`

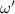
now its rotational kinetic energy is given by

`KE = (1)/(2)((1)/(2)MR^2)\omega'^2`

now if rotational kinetic energy of solid sphere is same as rotational kinetic energy of solid sphere then

`(1)/(2)((2)/(5)MR^2)\omega^2 = (1)/(2)((1)/(2)MR^2)\omega'^2`

`(2)/(5)\omega^2 = (1)/(2)\omega'^2`

`\omega' = 0.89\omega`