Question

Chris shoots an arrow up into the air. The height of the arrow is given by the function h(t) = - 16t2 + 64t + 23 where t is the time in seconds. What is the maximum height of the arrow?

Answer 1

Completing the square gives the answer right away.

`-16t^2+64t+23=-16(t^2-4t)+23=-16(t^2-4t+4-4)+23=-16((t-2)^2-4)+23`

`\implies h(t)=-16(t-2)^2+87`

which indicates a maximum height of 87 when
`t=2`.

Answer 2

The maximum height of the arrow is 87 meters.

Step-by-step explanation:

If we look at the height function of the arrow

`h(t)=-16t^(2) +64t+23`

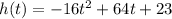
we see that its a parabola whose principal coefficient is negative, that means is inverted or upside down.

When the arrow reaches maximum height its velocity will be zero. The velocity of an object is the derivative of the position function, in this case the so called height function.

So we we derivate the height function to get that

`h'(t)=-32t+64`

we must find the t that makes this equation equal to zero:

`-32t+64=0`

`32t=64`

`t=2s`

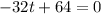
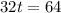
we replace this value of t in the height function:

`h(2 s)=-16.(2s)^(2) +64.(2s)+23`

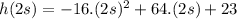
we get that

`h(2s)=87m`

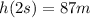
The maximum height of the arrow is 87 meters.

We have used the MKS system which uses the meter, kilogram and second as base units.