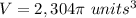Match each spherical volume to the largest cross sectional area of that sphere - Askians

Match each spherical volume to the largest cross sectional area of that sphere

asked Nov 24, 2020 106k views

2 Answers

Answer:

Part 1)
$324\pi\ units^(2)$ ------>
$7,776\pi\ units^(3)$

Part 2)
$36\pi\ units^(2)$ ------>
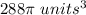
$288\pi\ units^(3)$

Part 3)
$81\pi\ units^(2)$ ------>
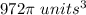
$972\pi\ units^(3)$

Part 4)
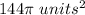$144\pi\ units^(2)$ ------>
$2,304\pi\ units^(3)$

Explanation:

we know that

The largest cross sectional area of that sphere is equal to the area of a circle with the same radius of the sphere

Part 1) we have

$A=324\pi\ units^(2)$

The area of the circle is equal to

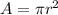
$A=\pi r^(2)$

so

$324\pi=\pi r^(2)$

Solve for r

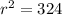
r^(2)=324

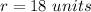
$r=18\ units$

Find the volume of the sphere

The volume of the sphere is

$V=(4)/(3)\pi r^(3)$

For
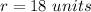
$r=18\ units$

substitute

$V=(4)/(3)\pi (18)^(3)$

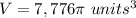
$V=7,776\pi\ units^(3)$

Part 2) we have

$A=36\pi\ units^(2)$

The area of the circle is equal to

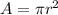
$A=\pi r^(2)$

so

$36\pi=\pi r^(2)$

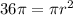
Solve for r

r^(2)=36

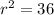
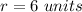
$r=6\ units$

Find the volume of the sphere

The volume of the sphere is

$V=(4)/(3)\pi r^(3)$

For
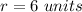
$r=6\ units$

substitute

$V=(4)/(3)\pi (6)^(3)$

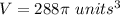
$V=288\pi\ units^(3)$

Part 3) we have

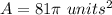
$A=81\pi\ units^(2)$

The area of the circle is equal to

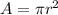
$A=\pi r^(2)$

so

$81\pi=\pi r^(2)$

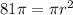
Solve for r

r^(2)=81

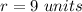
$r=9\ units$

Find the volume of the sphere

The volume of the sphere is

$V=(4)/(3)\pi r^(3)$

For
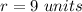
$r=9\ units$

substitute

$V=(4)/(3)\pi (9)^(3)$

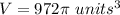
$V=972\pi\ units^(3)$

Part 4) we have

$A=144\pi\ units^(2)$

The area of the circle is equal to

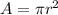
$A=\pi r^(2)$

so

$144\pi=\pi r^(2)$

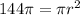
Solve for r

r^(2)=144

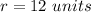
$r=12\ units$

Find the volume of the sphere

The volume of the sphere is

$V=(4)/(3)\pi r^(3)$

For
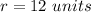
$r=12\ units$

substitute

$V=(4)/(3)\pi (12)^(3)$

$V=2,304\pi\ units^(3)$

Paxton answered Dec 1, 2020

by Paxton

8.0k points

← Prev Question Next Question →

Search Askians