Question

A bullet of mass 12 g strikes a ballistic pendulum of mass 2.2 kg. The center of mass of the pendulum rises a vertical distance of 10 cm. Assuming that the bullet remains embedded in the pendulum, calculate the bullet's initial speed.

Answer 1

The bullet's initial speed 258.06 m/s.

Step-by-step explanation:

It is given that,

It is given that,

Mass of the bullet, m₁ = 12 g = 0.012 kg

Mass of the pendulum, m₂ = 2.2 kg

The center of mass of the pendulum rises a vertical distance i.e. h = 10 cm = 0.1 m

We need to find the initial speed of the bullet. Here, the kinetic energy of the bullet gets converted to potential energy of the system as :

`(1)/(2)(m_1+m_2)V^2=(m_1+m_2)gh`

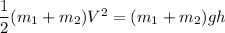
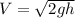`V=√(2gh)`....................(1)

Where

V is the speed of bullet and pendulum at the time of collision.

Let v be the initial speed of the bullet. Using conservation of momentum as :

`m_1v=(m_1+m_2)V`

`V=((m_1+m_2)/(m_1))√(2gh)`

`V=((0.012\ kg+2.2\ kg)/(0.012 kg))√(2* 9.8\ m.s^2* 0.1\ m)`

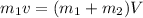
V = 258.06 m/s

So, the initial speed of the bullet is 258.06 m/s. Hence, this is the required solution.