Question

If r(x) = 2 – x2 and w(x) = x – 2, what is the range of (Wºr) (x)

(-∞,0]
(-∞,2]
[0,∞)
[2,∞)

Answer 1

(-inf,2]

Explanation:

`(w \circ r)(x)=w(r(x))`

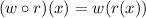
`w(2-x^2)` I replaced r(x) with 2-x^2

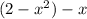`(2-x^2)-x` I replace the x in w(x)=x-2 with 2-x^2

`-x^2-x+2`

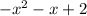
You can graph this to find the range.

But since this is a quadratic (the graph is a parabola), I'm going to find the vertex to help me to determine the range.

The vertex is at x=-b/(2a). Once I find x, I can find the y that corresponds to it by using y=-x^2-x+2.

Comparing ax^2+bx+c to -x^2-x+2 tells me a=-1, b=-1, and c=2.

So the vertex is at x=1/(2*-1)=-1/2.

To find the y-coordinate that corresponds to that I will not plug in -1/2 in place of x into -x^2-x+2.

This gives me

-(-1/2)^2-(-1/2)+2

-1/4 + 1/2 +2

Find a common denominator which is 4.

-1/4 + 2/4 +8/4

8/4

2.

So the highest y value is 2 ( I know tha parabola is upside down because a=negative number)

That mean then range is 2 or less than 2.

So the answer an interval notation is (-inf,2]