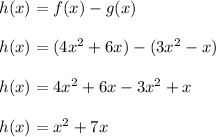Question

The area of two rectangles is given by he functions: area of a rectangle A:f(x)= 4x2+6x area of rectangle B:g(x)=3x2-x Which function represents the difference? A.h(x)=7x2-5x B.h(x)=x2-7x C.h(x)=x2+5x D.h(x)=x2+7x

Answer 1

x^2+7x if you are asked to find the difference of a function f and function g

Explanation:

We are asked to A-B or f(x)-g(x).

(4x^2+6x)-(3x^2-x)

4x^2+6x-3x^2+x

The like terms I'm going to pair up.

4x^2-3x^2+6x+x

1x^2 +7x

x^2 +7x

The answer is x^2+7x

Answer 2

OPTION D:
`h(x)=x^2+7x`

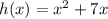
Explanation:

You know that the area of Rectangle A is given by :

`f(x)= 4x^2+6x`

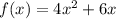
And the area of Rectangle B is given by:

`g(x)=3x^2-x`

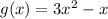
Therefore, in otder to find the function that represents the difference, you need to subtract the functions f(x) and g(x).

Then, you get this function h(x):

`h(x)=f(x)-g(x)\\\\h(x)= (4x^2+6x)-(3x^2-x)\\\\h(x)=4x^2+6x-3x^2+x\\\\h(x)=x^2+7x`