Question

The area of the triangle is given by the functions area of triangle A:x2 + x area of triangle B: x2 - 3x which functions represents the sum of the areas of the two triangles? 1. 4x 2.-4x 3.x2-4x 4.2x2-2x

Answer 1

4. 2x^2 - 2x.

Explanation:

Adding the 2 functions:

Area of the 2 triangles = x^2 + x + x^2 - 3x

= .2x^2 - 2x

Answer 2

OPTION 4

Explanation:

Let be f(x) the function that represents the area of Triangle A:

`f(x)=x^2 + x`

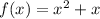
Let be g(x) the function that represents the area of Triangle B:

`g(x)=x^2 - 3x`

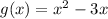
Then, you need to add the area of Triangle A and the area of Triangle B in order to find the sum of the areas (Let be h(x) the function that represents the sum of the the areas of triangles A and B):

Therefore, this is:

`h(x)=(x^2 + x)+(x^2 - 3x)=x^2 + x+x^2 - 3x=2x^2-2x`

You can notice that this matches with the option 4.