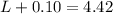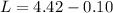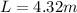Question

A 180-g block is pressed against a spring of force constant 1.35 kN/m until the block compresses the spring 10.0 cm. The spring rests at the bottom of a ramp inclined at 60.0° to the horizontal. Using energy considerations, determine how far up the incline the block moves from its initial position before it stops under the following conditions.

Answer 1

L = 4.32 m

Step-by-step explanation:

Here we can use the energy conservation to find the distance that it will move

As per energy conservation we can say that the energy stored in the spring = gravitational potential energy

`(1)/(2)kx^2 = mg(L + x)sin\theta`

`(1)/(2)(1.35 * 10^3)(0.10^2) = (0.180)(9.8)(L + 0.10)sin60`

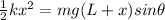
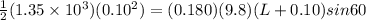
now we need to solve above equation for length L

`6.75 = 1.53(L + 0.10)`

`L + 0.10 = 4.42`

`L = 4.42 - 0.10`

`L = 4.32 m`