Question

Find b in the triangle shown.

2

3

4

5

Answer 1

4.97485 (approximately)

Explanation:

You have the information SAS given.

This is a case for law of cosines.

`b^2=a^2+c^2-2ac*cos(B)`

`b^2=12^2+10^2-2(12)(10)*cos(24)`

`b^2=144+100-240cos(24)`

`b^2=244-240cos(24)`

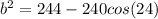
Take the square root

`b=√(244-240cos(24))`

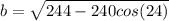
I was saving rounding to the end that is why I didn't put 240*cos(24) in my calculator.

So now I'm going to put sqrt(244-240*cos(24)) in my calculator. Make sure your calculator says deg (for degrees).

4.97485 (approximately)