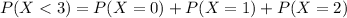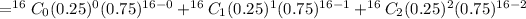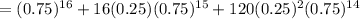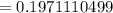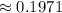Question

The centers for disease control and prevention reported that 25% of baby boys 6-8 months old in the united states weigh more than 20 pounds. A sample of 16 babies is studied. What is the probability that fewer than 3 weigh more than 20 pounds?

Answer 1

0.1971 ( approx )

Explanation:

Let X represents the event of weighing more than 20 pounds,

Since, the binomial distribution formula is,

`P(x)=^nC_r p^r q^(n-r)`

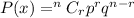
Where,
`^nC_r=(n!)/(r!(n-r)!)`

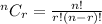
Given,

The probability of weighing more than 20 pounds, p = 25% = 0.25,

⇒ The probability of not weighing more than 20 pounds, q = 1-p = 0.75

Total number of samples, n = 16,

Hence, the probability that fewer than 3 weigh more than 20 pounds,

`P(X<3) = P(X=0)+P(X=1)+P(X=2)`

`=^(16)C_0 (0.25)^0 (0.75)^(16-0)+^(16)C_1 (0.25)^1 (0.75)^(16-1)+^(16)C_2 (0.25)^2 (0.75)^(16-2)`

`=(0.75)^(16)+16(0.25)(0.75)^(15)+120(0.25)^2(0.75)^(14)`

`=0.1971110499`

`\approx 0.1971`