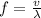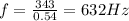Answer:
f = 632 Hz
Step-by-step explanation:
As we know that for destructive interference the path difference from two loud speakers must be equal to the odd multiple of half of the wavelength
here we know that
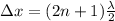
given that path difference from two loud speakers is given as
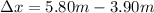
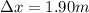
now we know that it will have fourth lowest frequency at which destructive interference will occurs
so here we have
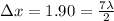
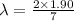
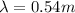
now for frequency we know that