Answer: t= 2.032
Explanation:
Given : Sample size :

Sample mean :
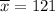
Standard deviation :

Claim : The IQ scores of statistics professors are normally distributed, with a mean greater than 116.
Let
 be the mean scores of statistics professors.
be the mean scores of statistics professors.
Then the set of hypothesis for the given situation will be :-
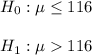
As the alternative hypothesis is right tailed , thus the test would be right tail test.
Since the sample size is less than 30, therefore the test would be t-test .
The test statistics for the given situation will be :-
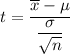
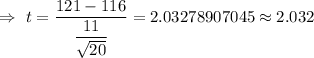
Hence, the value of the test statistic : t= 2.032