What is the change that occurs to the parent function f(x) = x^2 given the function f(x) = 2(x + 2)^2 + 1. The graph is compressed by a factor of 2, moves 2 units to the right, …

Question

asked Mar 16, 2020 179k views

1 Answer

Manuel Arwed Schmidt · Answer 1 · 2020-03-21T20:21:06+0000

Answer:

The graph is stretched by a factor of 2, moves 2 units to the left, and 1 unit up.

Explanation:

The base of the quadratic function is

$f(x) = {x}^(2)$

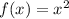
We can transform this function to look narrower or wider.

Looking narrower is termed a stretch.

This happens when a>1

Looking wider is termed a compression.

This happens when 0<a<1

We can also

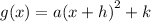
$g(x) = a {(x + h)}^(2) + k$

+h moves the parent graph to the left by h units

-h moves the parent graph to the left by h units.

+ k moves the parent function up by k units

- k moves the parent function down by k units.

The change that occurs to

$f(x) = {x}^(2)$

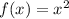
given

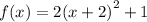
$f(x) = 2( {x + 2)}^(2) + 1$

is that, the graph is stretched by a factor of 2, moves 2 units to the left, and 1 unit up

Therefore the last choice is the correct answer.