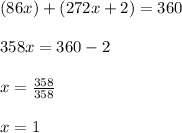Answer:

Explanation:
In order to find the value of "x", it is important to remember that:

We can identify in the figure that:
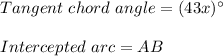
Then:
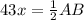
Solving for AB:
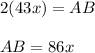
Now, since there are 360° in a circle, we know that:

Then we can substitute
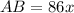 into
into
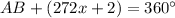 and solve for "x". This is:
and solve for "x". This is: