Answer:
Option B) a = 1, b = 3, c = 4
Explanation:
We are given the following information in the question:
We are given an expression:

The solving of the above expression can be done in the following manner:
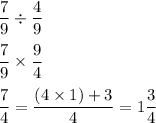
Comparing the right side of the expression, we have,
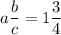
Comparing, we get,
a = 1, b = 3, c = 4
Option B) s the correct option.