Question

A gas of helium atoms (each of mass 6.65 × 10-27 kg) are at room temperature of 20.0°C. What is the de Broglie wavelength of the helium atoms that are moving at the root-mean-square speed? (h = 6.626 × 10-34 J · s, the Boltzmann constant is 1.38 × 10-23 J/K)

Answer 1

The de Broglie wavelength of the helium atoms is
`7.373*10^(-11)\ m`.

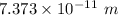Step-by-step explanation:

Given that,

Mass
`M=6.65*10^(-27)\ kg`

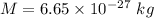
Temperature = 20.0°C

We need to calculate the root-mean square speed

Using formula of root mean square speed

`v_(rms)=\sqrt{(3kTN_(A))/(M)}`

Where, N = Avogadro number

M = Molar mass

T = Temperature

k = Boltzmann constant

Put the value into the formula

`v_(rms)=\sqrt{(3*1.38*10^(-23)*293*6.022*10^(23))/(4*10^(-3))}`

`v_(rms)=1351.37\ m/s`

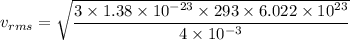
We need to calculate the de Broglie wavelength

Using formula of de Broglie wavelength

`P=(h)/(\lambda)`

`mv=(h)/(\lambda)`

`\lambda=(6.626*10^(-34))/(6.65*10^(-27)*1351.37)`

`\lambda=7.373*10^(-11)\ m`

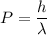
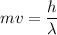
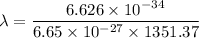
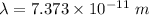
Hence, The de Broglie wavelength of the helium atoms is
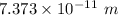`7.373*10^(-11)\ m`.