Answer:
1. B. a=14, b=2
2. D. a=1, b=1.4
Explanation:
The exponential growth function can be represented as
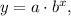
where b is the growth factor.
1. When the function has equation
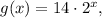
then
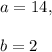
The initial amount is the value of the function at x=0:
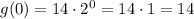
The growth factor is b=2
2. When the function has equation

then
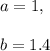
The initial amount is the value of the function at t=0:

The growth factor is b=1.4