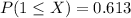Compute the following binomial probabilities directly from the formula for b(x; n, p). (Round your answers to three decimal places.) (a) b(5; 8, 0.25) .023 (b) b(6; 8, 0.65) .25…

Question

asked May 9, 2020 150k views

1 Answer

Katedral Pillon · Answer 1 · 2020-05-15T09:50:23+0000

We know that the binomial theorem for finding the probability of x success out of a total of n experiments is given by:

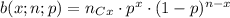
$b(x;n;p)=n_C_x\cdot p^x\cdot (1-p)^(n-x)$

(a)

b(5; 8, 0.25)

is given by:

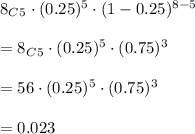
$8_C_5\cdot (0.25)^5\cdot (1-0.25)^(8-5)\\\\=8_C_5\cdot (0.25)^5\cdot (0.75)^3\\\\=56\cdot (0.25)^5\cdot (0.75)^3\\\\=0.023$

Hence, the answer is: 0.023

(b)

b(6; 8, 0.65)

i.e. it is calculated by:

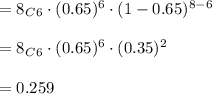
$=8_C_6\cdot (0.65)^6\cdot (1-0.65)^(8-6)\\\\=8_C_6\cdot (0.65)^6\cdot (0.35)^2\\\\=0.259$

Hence, the answer is: 0.259

(c)

P(3 ≤ X ≤ 5) when n = 7 and p = 0.55

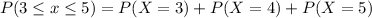
$P(3\leq x\leq 5)=P(X=3)+P(X=4)+P(X=5)$

Now,

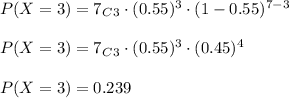
$P(X=3)=7_C_3\cdot (0.55)^3\cdot (1-0.55)^(7-3)\\\\P(X=3)=7_C_3\cdot (0.55)^3\cdot (0.45)^(4)\\\\P(X=3)=0.239$

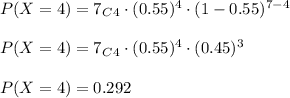
$P(X=4)=7_C_4\cdot (0.55)^4\cdot (1-0.55)^(7-4)\\\\P(X=4)=7_C_4\cdot (0.55)^4\cdot (0.45)^(3)\\\\P(X=4)=0.292$

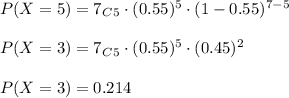
$P(X=5)=7_C_5\cdot (0.55)^5\cdot (1-0.55)^(7-5)\\\\P(X=3)=7_C_5\cdot (0.55)^5\cdot (0.45)^(2)\\\\P(X=3)=0.214$

Hence,

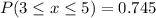
$P(3\leq x\leq 5)=0.745$

(d)

P(1 ≤ X) when n = 9 and p = 0.1 .613

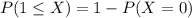
$P(1\leq X)=1-P(X=0)$

Also,

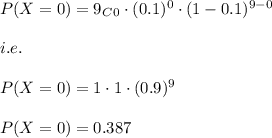
$P(X=0)=9_C_0\cdot (0.1)^(0)\cdot (1-0.1)^(9-0)\\\\i.e.\\\\P(X=0)=1\cdot 1\cdot (0.9)^9\\\\P(X=0)=0.387$

i.e.

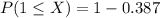
$P(1\leq X)=1-0.387$

Hence, we get:

$P(1\leq X)=0.613$