Answer:
A(2,2)
Explanation:
Let the vertex A has coordinates
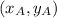
Vectors AB and AB' are perpendicular, then
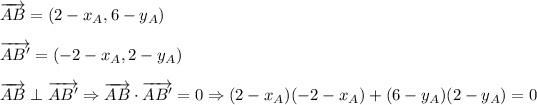
Vectors AC and AC' are perpendicular, then
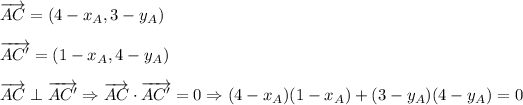
Now, solve the system of two equations:
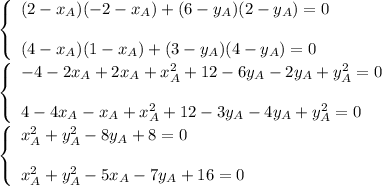
Subtract these two equations:
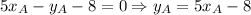
Substitute it into the first equation:
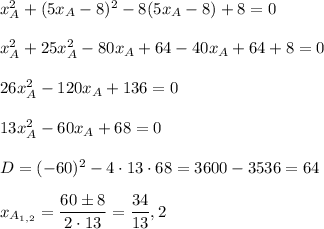
Then
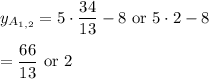
Rotation by 90° counterclockwise about A(2,2) gives image points B' and C' (see attached diagram)