Question

Assume that​ women's heights are normally distributed with a mean given by mu equals 62.5 in​, and a standard deviation given by sigma equals 2.5 in. ​(a) If 1 woman is randomly​ selected, find the probability that her height is less than 63 in. ​(b) If 35 women are randomly​ selected, find the probability that they have a mean height less than 63 in. ​(​a) The probability is approximately nothing. ​(Round to four decimal places as​ needed.) ​(b) The probability is approximately nothing. ​(Round to four decimal places as​ needed.)

Answer 1

Answer: a) The probability is approximately = 0.5793

b) The probability is approximately=0.8810

Explanation:

Given : Mean :
`\mu= 62.5\text{ in}`

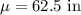
Standard deviation :
`\sigma = \text{2.5 in}`

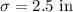
a) The formula for z -score :

`z=(x-\mu)/((\sigma)/(√(n)))`

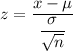
Sample size = 1

For x= 63 in. ,

`z=(63-62.5)/((2.5)/(√(1)))=0.2`

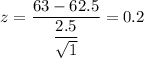
The p-value =
`P(z<0.2)=`

`0.5792597\approx0.5793`

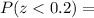
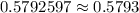
Thus, the probability is approximately = 0.5793

b) Sample size = 35

For x= 63 ,

`z=(63-62.5)/((2.5)/(√(35)))\approx1.18`

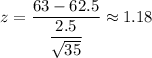
The p-value =
`P(z<1.18)`

`= 0.8809999\approx0.8810`

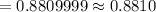
Thus , the probability is approximately=0.8810.