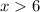For this case we have the following inequality:
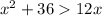
We subtract 12x on both sides of the inequality:

We convert to an equation:
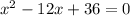
To factor the equation, we must find two numbers that when multiplied give +36 and when added together obtain -12. These numbers are -6 and -6.
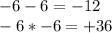
So, we have:
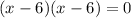
The solution is
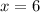
We create test intervals:
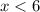
We test a value in the interval, such as x = 0:
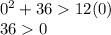
Is fulfilled!
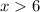
We test a value in the interval, such as x = 10.

Is fulfilled!
Thus, the solution is given by:
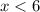 or
or
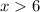
Answer:
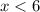 or
or