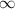Question

15. Determine the zeros for and the end behavior of f(x) = x(x - 4)(x + 2)

Answer 1

`x=0\\x=4\\x=-2`

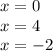
Step-by-step explanation:

The zeros of a function are all the values of x for which f (x) = 0.

Therefore to find the zeros of the function I must equal f(x) to zero and solve for x.

`f(x) = x(x - 4)(x + 2)=0`

`x(x - 4)(x + 2)=0`

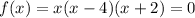
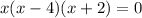
We have the multiplication of 3 factors x, (x-4) and (x + 2)

Then the function will be equal to zero when one of the factors is equal to zero, that is:

`x = 0\\(x-4) = 0,\ x = 4\\(x + 2) = 0,\ x = -2`

Note that
`f(x) = x (x - 4) (x + 2)` is a cubic function of positive principal coefficient, the graph starts from
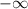`-\infty` and cuts to the x-axis at
`x = -2`, then decreases and cuts by second once to the x-axis at
`x = 0`, it finally cuts the x-axis for the third time at
`x = 4` and then tends to
`\infty`