Question

A solid nonconducting sphere of radius R carries a charge Q distributed uniformly throughout its volume. At a certain distance r1 (r1 < R) from the center of the sphere, the electric field has magnitude E. If the same charge Q were distributed uniformly throughout a sphere of radius 2R, the magnitude of the electric field at the same distance r1 from the center would be equal to:

Answer 1

`E' = (E)/(8)`

Step-by-step explanation:

As we know that that electric field inside the solid non conducting sphere is given as

`\int E.dA = (q_(en))/(\epsilon_0)`

`\int E.dA = ((Q)/(R^3)r_1^3)/(\epsilon_0)`

`E(4\pi r_1^2) = (Qr_1^3)/(R^3 \epsilon_0)`

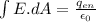
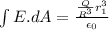
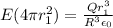
so electric field is given as

`E = (Qr_1)/(4\pi \epsilon_0 R^3)`

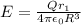
now if another sphere has same charge but twice of radius then the electric field at same position is given as

`E' = (Qr_1)/(4\pi \epsilon_0 (2R)^3)`

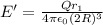
so here we have

`E' = (E)/(8)`