Answer: The correct option is (B) 3.
Step-by-step explanation: We are given a circle X with radius 5 units and chord AB with length 8 units.
We are to find the length of segment XC that bisects chord.
We know that the line segment drawn from the center of a circle to the midpoint of a chord is perpendicular to the chord.
So, in the given circle X, the segment XC is perpendicular to chord AB. Then, triangle XCB will be a right angled triangle with hypotenuse XB.
Since XC bisects AB, so the length of BC will be
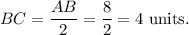
And, radius, XB = 5 units.
Using Pythagoras theorem in triangle XCB, we have
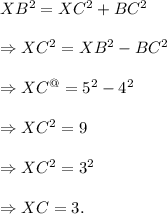
Thus, the length of the segment XC is 3 units.
Option (B) is CORRECT.