Question

Given circle X with radius 5 units and chord AB with length 8 units, what is the

length of segment XC, which bisects the chord?

Answer 1

B. 3

Explanation:

just took the test :)

Answer 2

Answer: The correct option is (B) 3.

Step-by-step explanation: We are given a circle X with radius 5 units and chord AB with length 8 units.

We are to find the length of segment XC that bisects chord.

We know that the line segment drawn from the center of a circle to the midpoint of a chord is perpendicular to the chord.

So, in the given circle X, the segment XC is perpendicular to chord AB. Then, triangle XCB will be a right angled triangle with hypotenuse XB.

Since XC bisects AB, so the length of BC will be

`BC=(AB)/(2)=(8)/(2)=4~\textup{units}.`

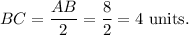
And, radius, XB = 5 units.

Using Pythagoras theorem in triangle XCB, we have

`XB^2=XC^2+BC^2\\\\\Rightarrow XC^2=XB^2-BC^2\\\\\Rightarrow XC^@=5^2-4^2\\\\\Rightarrow XC^2=9\\\\\Rightarrow XC^2=3^2\\\\\Rightarrow XC=3.`

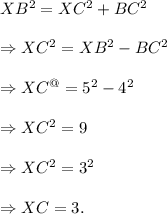
Thus, the length of the segment XC is 3 units.

Option (B) is CORRECT.