Answer:0.2 rad/s
Step-by-step explanation:
Given data
Velocity of the bottom point of the ladder=1.2Ft/s
Length of ladder=10ft
distance of the bottom most point of ladder from origin=8ft
From the data the angle θ with ladder makes with horizontal surface is
Cosθ=
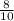
θ=36.86≈37°
We have to find rate of change of θ
From figure we can say that
 +
+
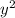 =
=
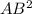
Differentiating above equation we get
 =-
=-
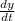
i.e
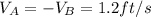
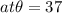
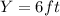

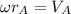

ω=0.2rad/s
i.e.Rate of change of angle=0.2 rad/s