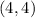Question

The first two steps in determining the solution set of the system of equations y=x^2-6x

+12 and y=2x-4. Which represents the solution(s) of this system of equations?

Answer 1

For this case we have the following system of equations:

`y = x ^ 2-6x + 12\\y = 2x-4`

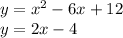
Equating the equations:

`x ^ 2-6x + 12 = 2x-4\\x ^ 2-6x-2x + 12 + 4 = 0\\x ^ 2-8x + 16 = 0`

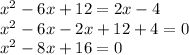
We look for two numbers that when multiplied, get 16, and when added together, get -8.

These numbers are -4 and -4.

`(x-4) (x-4) = 0\\(x-4) ^ 2 = 0`

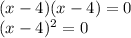
So, the solution is
`x = 4`

We look for the value of y:

`y = 2x-4\\y = 2 (4) -4\\y = 8-4\\y = 4`

Finally, the solution is:
`(4,4)`

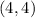
ANswer:

`(4,4)`