Answer:
69.7 feet.
Explanation:
Let x represent the distance between vulture and roadkill.
We have been given that a vulture is perched 40 ft up in a tree and looks down at an angle of depression of a 35 and spots roadkill.
We can see from the attachment that vulture, roadkill and angle of depression forms a right triangle with respect to ground, where, x is hypotenuse and 40 ft is opposite side.
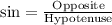
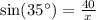
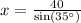
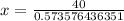
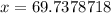
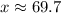
Therefore, the roadkill is 69.7 feet away from the vulture.