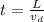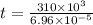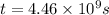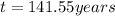Question

A 310-km-long high-voltage transmission line 2.00 cm in diameter carries a steady current of 1,190 A. If the conductor is copper with a free charge density of 8.50 1028 electrons per cubic meter, how many years does it take one electron to travel the full length of the cable

Answer 1

t = 141.55 years

Step-by-step explanation:

As we know that the radius of the wire is

r = 2.00 cm

so crossectional area of the wire is given as

`A = \pi r^2`

`A = \pi(0.02)^2`

`A = 1.26 * 10^(-3) m^2`

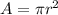
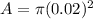
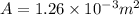
now we know the free charge density of wire as

`n = 8.50 * 10^(28)`

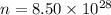
so drift speed of the charge in wire is given as

`v_d = (i)/(neA)`

`v_d = (1190)/((8.50 * 10^(28))(1.6 * 10^(-19))(1.26* 10^(-3)))`

`v_d = 6.96 * 10^(-5) m/s`

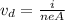
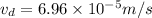
now the time taken to cover whole length of wire is given as

`t = (L)/(v_d)`

`t = (310 * 10^3)/(6.96 * 10^(-5))`

`t = 4.46 * 10^9 s`

`t = 141.55 years`