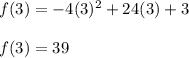Question

Consider f(x) = -4x2 + 24x + 3. Determine whether the function has a maximum or minimum value. Then find the

value of the maximum or minimum

Answer 1

The function has a maximum in
`x=3`

The maximum is:

`f(3) = 39`

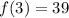
Step-by-step explanation:

Find the first derivative of the function for the inflection point, then equal to zero and solve for x

`f(x)' = -4*2x + 24=0`

`-4*2x + 24=0`

`8x=24`

`x=3`

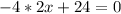
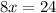
Now find the second derivative of the function and evaluate at x = 3.

If
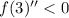`f (3) ''< 0` the function has a maximum

If
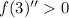`f (3) '' >0` the function has a minimum

`f(x)''= 8`

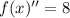
Note that:

`f(3)''= -8<0`

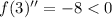
the function has a maximum in
`x=3`

The maximum is:

`f(3)=-4(3)^2+24(3) + 3\\\\f(3) = 39`