Question

An automobile tire has a radius of 0.344 m, and its center moves forward with a linear speed of v = 20.1 m/s. (a) Determine the angular speed of the wheel. (b) Relative to the axle, what is the tangential speed of a point located 0.135 m from the axle?

Answer 1

The angular speed and tangential speed are 58.69 rad/s and 7.92 m/s.

Step-by-step explanation:

Given that,

Radius = 0.344 m

Speed v= 20.1 m/s

(I). We need to calculate the angular speed

Firstly we will calculate the time

Using formula of time

`t = (d)/(v)`

`t=(2\pi* r)/(v)`

`t =(2*3.14*0.344)/(20.1)`

`t=0.107`

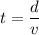
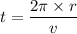
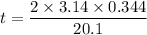
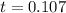
The angular velocity of the tire

`\omega=(2\pi)/(t)`

`\omega=(2*3.14)/(0.107)`

`\omega=58.69\ rad/s`

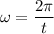
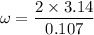
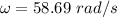
Now, using formula of angular velocity

(II). We need to calculate the tangential speed of a point located 0.135 m from the axle

The tangential speed

`v = r\omega`

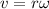
Where,

r = distance

`\omega`= angular velocity

Put the value into the formula

`v= 0.135*58.69`

`v=7.92\ m/s`

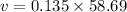
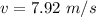
Hence, The angular speed and tangential speed are 58.69 rad/s and 7.92 m/s.