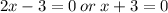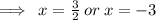Question

Find the roots of the parabola given by the following equation.

2x^2+ 5x - 9 = 2x
Show work please!

Answer 1

`2x^(2)+5x-9=2x\\2x^(2)+3x-9=0\\(x+3)(2x-3)=0\\\boxed{x=-3,(3)/(2)}`

Answer 2

`x = (3)/(2) \: or \: x = - 3`

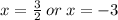
Step-by-step explanation

We want to find the roots of the parabola with equation:

`2 {x}^(2) + 5x - 9 = 2x`

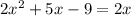
We need to write this in the standard quadratic equation form.

We group all terms on the left to get:

`2 {x}^(2) + 5x - 2x - 9 = 0`

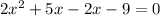
We simplify to get:

`2 {x}^(2) +3x- 9 = 0`

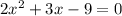
We now compare to:

`a {x}^(2) + bx + c = 0`

`\implies \: a = 2 , \: \: b = 3 \: \: and \: c=- 9`

`\implies ac = 2 * - 9 = - 18`

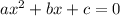
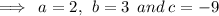
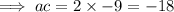
The factors of -18 that sums up to 3 are -3, 6.

We split the middle term with these factors to get:

`2 {x}^(2) +6x - 3x- 9 = 0`

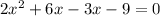
Factor by grouping:

`2x(x + 3) -3(x + 3) = 0`

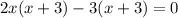
Factor again to obtain:

`(2x - 3)(x + 3) = 0`

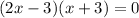
Apply the zero product principle to get:

`2x - 3 = 0 \: or \: x + 3 = 0`

`\implies \: x = (3)/(2) \: or \: x = - 3`